이 글은 체계적인 정리보다는 메모에 가깝습니다.
해당 논문에 대해 이야기 나누고 싶으시다면 언제든지 환영합니다.
Fast Model Editing at Scale
Eric Mitchell et al., 2023
https://openreview.net/forum?id=0DcZxeWfOPt
Fast Model Editing at Scale
While large pre-trained models have enabled impressive results on a variety of downstream tasks, the largest existing models still make errors, and even accurate predictions may become outdated...
openreview.net
요약
- MEND는 Hyper-Network Editor를 이용해 사전학습 모델에 정보를 업데이트 한다.
- MEND는 실제 내부 파라미터에 변화를 준다.
- MEND는 Rank-1 방식을 이용해 학습 속도를 향상시켰다.
Grounding

다음과 같이 MLP의 Layer l 과 Layer l+1이 있다고 가정하면

해당 그림이 두 layer 사이의 weight matrix가 된다.(그림과 같은 경우 n = 4)

역전파는 다음과 같이 chain rule을 통해 $\delta^{l+1}$와 $u^l$ 의 product로 $\nabla W$를 계산하는 형태를 전제
INTRODUCTION
새로운 knowledge를 학습하면 기존의 W는 (W+▽W)가 되는데 목표는 ▽W를 어떻게 효율적으로 구하는 것이 아래의 4가지 관점
- reliability
- post-edit model predicts the edit label ye for the edit input xe
- locality
- disagreement between the pre- and post- edit models on unrelated samples
- generality
- post-edit model predicts the label y′e when conditioned on x′e, for(x′e, y′e) ∈ N(xe, ye)
- efficiency
- the time and memory requirements for computing ϕ and evaluating E are small
에서 유리할지이다.
기존의 editor는 base model에서 역전파를 통해 $\nabla W$를 우선 계산하고(update는 하지 않고) 해당 $\nabla W$를 MLP model editor($g$)에 input으로 넣어 $\nabla\tilde{W}$를 계산하는 것이 목적이다.
기존의 방식 1 (Hu et al, 2021 LoRa)
base model의 $W$는 는 $d_d$ (if Fully Connected) 차원이기 때문에 $\nabla W$는 $d_d$차원이고
$\nabla\tilde{W}$를 rank-1으로 낮춰 $(d+d)$차원의 output으로 구성후 outer product한다면
model editor($g$)의 weight matrix는 $d^2(d+d) = 2d^3$ 차원이 될 것이다.

기존의 방식 2 (Raffel et al, 2020 T5)
복잡성을 줄이기 위해 rank r을 도입해 한 층을 쌓는다면
model editor($g$)의 weight matrix는 $r(d^2 + 2d)$ 차원이 될 것이다.

그러나 여전히 $d \approx 10^4$ 에 가까우므로 계산량이 크다.
METHOD
MEND의 해결방법
모델에 input으로 넣는 $\nabla W$는 역전파에 의해 $\nabla_{w_{l}}L = \Sigma_{i=1}^{B}\delta_{l+1}^{i}u_l^{i\intercal}$ 와 같이 계산된다.
(B = batch size, $\delta$ = gradient of the loss w.r.t. the preactivations at layer $l+1$, $u$ = inputs to layer $l$)
역전파 계산의 방식 자체가 $\nabla W$는 이미 decomposition되어 있는 rank-1 matrix라는 것을 시사하므로 이러한 원리에서 착안하여 각 벡터 $\delta_{l+1}^{i}, u_l^{i\intercal}$를 input으로 넣는다면 $d^2$차원의 input을 $2d$차원으로 줄일 수 있다.

따라서 논문에서는 $\nabla W$를 받아 $\nabla\tilde{W}$를 계산하는 editor가 아닌, 역전파 과정에서 계산된
$\delta_{l+1}^{i}, u_l^{i}$를 바로 받아 $\tilde\nabla_{w_{l}}L = \Sigma_{i=1}^{B}\tilde\delta_{l+1}^{i}\tilde u_l^{i\intercal}$를 output으로 계산하여 generality의 loss 없이 파라미터 수를 획기적으로 낮췄다.
또한 raw fine-tuning gradient는 useful한 starting point for editing이기 때문에 모델 residual connection을 사용하였다.(He et al, 2016)
최종 모델은 아래와 같다.
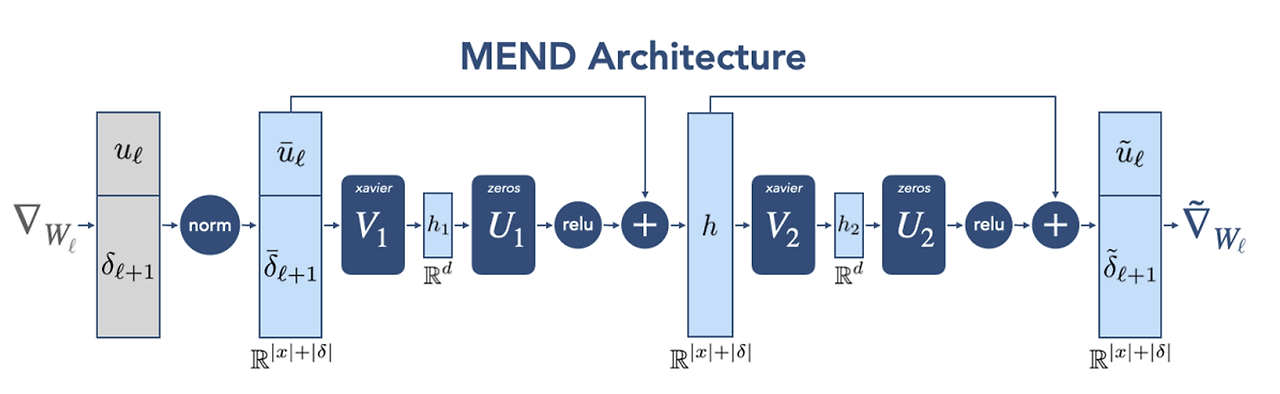
$h_l = z_l + \sigma(s_l^1 \circ (U_1 V_1 z_l + b) + o_l^1), \quad g(z_l) = h_l + \sigma(s_l^2 \circ U_2 V_2 h_l + o_l^2)$
Xavier 초기화는 균등분포 U(-a, a)를 통해 초기화하는 기법 이 때 a는 아래와 같다.

$\sigma$ = non-linear activation function, 논문에서는 RELU
$U_j, V_j$ = low rank factorization of MEND’s weights at layer j
- MEND의 total parameter를 O(d)로 맞추기 위함
- U1, U2는 initializing with zeros
- V1, V2는 Xavier uniform initialization(Glorot and Bengio, 2010)
$o_l, s_l$은 각각 기존 layer들의 크기를 맞춰주는 과정으로 해당 과정을 통해 MEND는 단일 모델에 대해 통합된 editor를 가질 수 있다.
최종적으로 Final weight matrix $\tilde W = W_l - \alpha\tilde\nabla_{w_l}$ 의 형태로 editing 된다.
($\alpha_l$ = learned per-layer(scalar) stap size)
TRAINING

edit example = $(x_e, y_e)$
locality example = $x_{loc}$
exuivalence examples = $(x_e', y_e')$
training loss(edit) = $L_e$
training loss(local) = $L_{loc}$ (KL divergence between the pre-edit and post-edit model on the locality input $x_{loc}$)
Total training loss = $c_{edit}L_e(\theta_{\tilde w}) + L_{loc}(\theta_{w}, \theta_{\tilde w})$
($c_e$ = 0.1 for all experiments, use Adam optimizer)
Conceptual comparisons

대표 방법론(ENN, KE)와 기존 Fine-tuning(FT), KL divergence를 통한 Fine-tuning(FT+KL) 비교
ENN(Editable Neural Networks, Sinitsin et al. 2020)
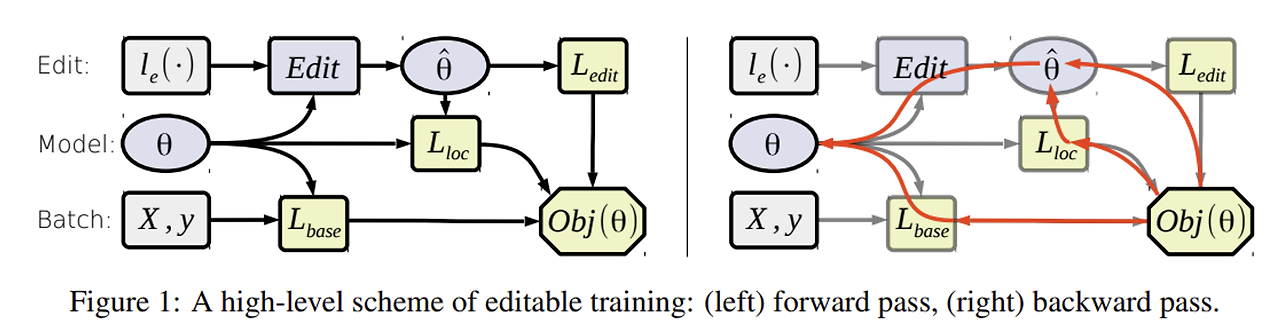
- ENN은 기존의 pre-trained 모델을 별도 저장한 상태에서 해당 모델에서 $\nabla W$를 계산 후 복사한 모델에 적용시키는 형태를 사용하므로 용량을 많이 차지하고 high-order의 gradient를 계산
- CV 분야 knowledge editing 논문
KE(Knowledge Editor, De Cao et al. 2021)

- KE는 똑같이 rank-1을 사용하지만 RNN 모델을 사용함
Experiments
4개의 실험 진행
- Editing very large transformers models
- smaller scale editing
- batched editing
- ablations & MEND variants
Metrics
Reliability & generality = ES(Edit success)

Locality = drawdown(perplexity increase or accuracy decrease)
1. Editing very large transformers models

MEND provides the most successful edits across tasks
KL_constrained fine-tuning은 perplexity 감소에서 강한 모습을 보여주었지만, 매우 큰 cost가 필요함
KE의 경우 대형 모델에서 성능이 매우 저조했다.
(ENN은 computation 용량의 한계로 실험 못함)
data

2. Smaller scale editing

전체적으로 작은 모델을 사용하다보니 overfitting되어 Fine-tuning 기반 모델의 성능이 저조하다.
Wikitext generation 문제의 경우 난이도가 높아 대부분의 모델이 저조한 성능을 보인다.
ENN의 경우 작은 모델에서 강력한 성능을 보인다.
3. Batched editing
여러개의 데이터를 editing

MEND는 단일 데이터에 대한 수정을 다룬 방법이므로 해당 실험에서는 단순히 edit 수만큼 파라미터를 업데이트한다.
학습하는 양이 많아질수록 MEND가 더 강력한 성능을 보인다.
(Accuracy down에 대해서, ENN이 더 준수한 성능을 보여주지만, ES의 측면에서 확연히 저조하기 때문에 MEND가 유리)
4. Ablations & MEND variants

‘No sharing’은 layer마다 개별적인 editor 생성(N = Num of layers)
‘No ID init’은 Xavier 초기화 대신 zero initialization을 의미한다.
Only $u_l, \delta_{l+1}, smaller$ 부분에 대해서 구체적으로 논문에 방식이 언급되지는 않았지만, $\tilde{u}$만 계산 후 $\delta_{l+1}$에 곱하는 형태로 진행했을 것으로 추정된다.
$m+n \approx 10^5, min(m,n) \approx 10^4$
MEND는 축소된 버전에서도 좋은 성능을 보여준 것으로 보어 점점 커지는 모델에도 적용할 여지가 있다.
Conclusion
- MEND는 매우 큰 모델에서도 효율적인 성능을 보여주는 접근법이다.
- MEND는 model editing problem을 learning problem으로 접근한다.
- relatively small edit dataset으로 실험하였다.
- single input-ouput pair에 대해서만 적용하는 방법론이다.
Limitations & Future Work
- MEND를 포함한 현재의 editor 기반 방법론은 전반적으로 over-generalization되어 locality examples(e.g. negative samples)에 대해서는 개선할 부분이 많음
- 현재의 generalization dataset은 일반적으로 back-translation을 이용함
개인 의견
- 해당 논문은 knowledge를 주입하는 것만 다루었음 → 삭제하는 것에 대한 추가 연구 필요
- 해당 논문은 단일 knowledge editing에 대해서만 다룸(multiple 상황에서는 단순 summation) → 좀더 복합적인 상황에 맞춰 발전 필요
- MEND는 MLP로 이루어져 있고 attention block과의 실험만 진행했는데 해당 구조가 완벽하진 않을것이라고 생각함
Q1. layer마다 차원이 다른데 MEND의 차원은 어떻게 맞추나?
A1. MEND learns separate set of editor parameters for each unique shape of weight matrix to be edited(p4). 각 layer마다 별도의 모델을 학습한다. 이 때 모든 layer를 할 필요는 없다.(논문에서는 BART, T5 모델은 each encoder, decoder의 last 2 transformer block을, 다른 모델은 last 3 transformer block를 edit)
Q2. 기존 모델의 fine-tuning보다 계산량 측면에서 무엇이 나은가?
A2. Note that we do not compute any higher-order gradients, because we do not optimize the pre-edit model parameters(p4). 기존 모델 fine-tuning은 상기한대로 $d^3$차원의 계산량을 요한다. + A1의 연장선으로, 원하는 layer만 계산하면 전체 모델 계산보다 줄어듦.
Q3. 왜 MLP로 구성했는가?
A3. Attention 기반 모델로 비교했을 때 MLP 성능이 더 좋았음.

'논문리뷰 > Knowledge Editing' 카테고리의 다른 글
| [논문 리뷰] Mass-Editing Memory In a Transformer (1) | 2024.01.25 |
|---|---|
| [논문 리뷰] Transformer-Patcher: One Mistake Worth One Neuron (1) | 2024.01.25 |
| [논문 리뷰] Can We Edit Factual Knowledge by In-Context Learning? (1) | 2024.01.25 |